



初めまして、横浜国立大学フォーミュラプロジェクトにおいて16年度にテクニカルディレクターをしていた堀と申します。
今回は、マニアな方々へ向けたコラムです。摩擦理論のような、少しだけニッチな点も攻めさせてゆきます。ゆるい文を書くのは苦手なため、以降は堅い文体でゆきますがご容赦ください(笑)。
また、一部工学を学んだ方向けに数式等も含ませていただきました。興味がなければ、飛ばしながらお読みください。

グリップ能力が高いスリックタイヤ
自動車に外力を加える物体は、路面と空気だけである。さらにこの二つの力においても、支配的となるのは路面からの力、つまりタイヤの摩擦力である。
現代の車両、特にレーシングカーにおいては空力、つまり空気からの外力が重要視されているが、ダウンフォースはタイヤの摩擦力を向上させるために用いられており、タイヤの重要性がうかがえる。
タイヤの構造について簡単に述べる。
タイヤはただのゴムの塊ではなく、内部は層構造となっている。表面のゴム部分の下には、ベルト、カーカス(プライの層)、インナーライナーと呼ばれる部分が納められている。また、各部を図1のように呼ぶ。
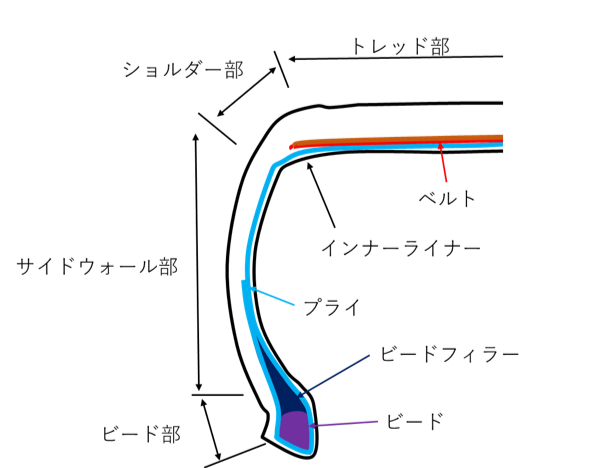
図1 タイヤの断面図の概略(ラジアルタイヤ、半分のみ)
プライの層である“カーカス”の方向によって、タイヤの名称が変わる。
・カーカスが、タイヤに対して縦、横に設置されているものを“ラジアルタイヤ”
・カーカスが、タイヤに対して斜め方向に設置されているものを“バイアスタイヤ”
と呼ぶ。
バイアスタイヤには、剛性確保のためのベルトやビードフィラーが使われない。ラジアルタイヤは、剛性を持たせる部品を分離することでロスを少なく出来る。現代の車両はほとんど“ラジアルタイヤ”である。“バイアスタイヤ”は、かつては主流であったが、現在ではレーシングカートなど一部のものにしか用いられない。
タイヤが発生する力の静特性について簡単に記述する。
タイヤが発生するせん断力は加減速時に代表される前後力(Longitudinal force、Fx)と旋回時に代表される横力(Lateral force、Fy)に分けられ、いずれもタイヤの変形によって力が生じる。
前後力の発生の図を、図2に示す。図2、3において力の方向は、地面に加える力(車に加わる力と逆方向)の方向を矢印で表した。
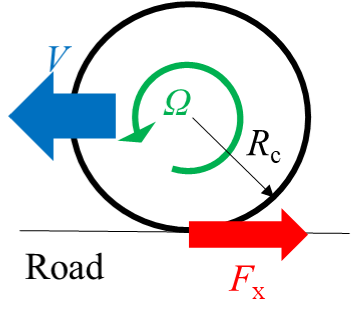
図2 前後力発生の概略
前後力は主にスリップ率κの関数として表せる。
スリップ率は(1)式で定義する。
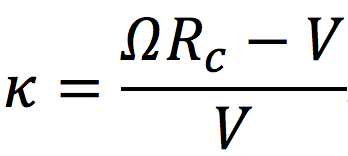
(1)式 Rc=タイヤ半径/Ω=タイヤ回転速度/V=車速
次に、横力の発生の図を、図3に示す。
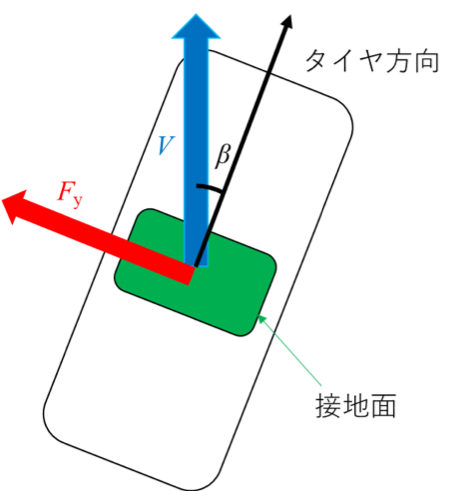
図3 横力発生の概略
横力は主に(キャンバー角や路面等の影響を無視)各輪のスリップアングルβiの関数として表せる。
スリップアングルは“タイヤの”速度方向と向きの角度の関数である。
車両全体においては(2)式で定義される。(各輪における±の符号は省略した)
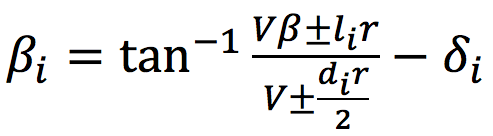
(2)式
V=車両速度/β=車体スリップアングル/li=重心からアクスルまでの距離/di=トラック/r=ヨー速度/δi=各輪舵角(ジオメトリ、コンプライアンス等含
前後力、横力についてグラフで示すと次のようになる。
図4及び図5は、前後左右いずれかの力しか発生していない状態であり、Pure slipと呼ぶ。
Magic Formulaと呼ばれる車両運動解析に用いられる式からグラフは作成しており、パラメータは適当なものを用いた。
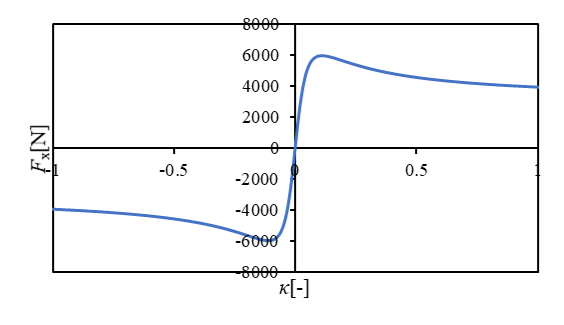
図4 スリップ率に対する前後力の変化
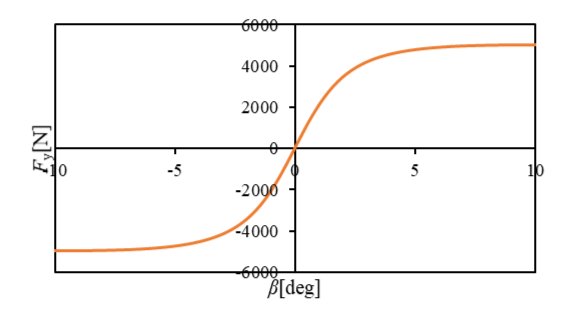
図5 スリップアングルに対する横力の変化
ここで、スリップ率、スリップアングルがそれぞれ小さいとき、力はそれらの比例関数と扱えることがわかる。
この部分を以降、線形域と呼び、比例関係とならない部分を非線形域と呼ぶ。
線形域におけるスリップアングル1 deg(もしくは1 rad)あたりの横力をコーナリングパワー(Cornering stiffness)と呼ぶ。
さらに、横力発生時の接地面について考えてみる。
Vはタイヤの進行方向である接地面は、次の図6のようになっており、滑り域と接着域が混在していることがわかる。
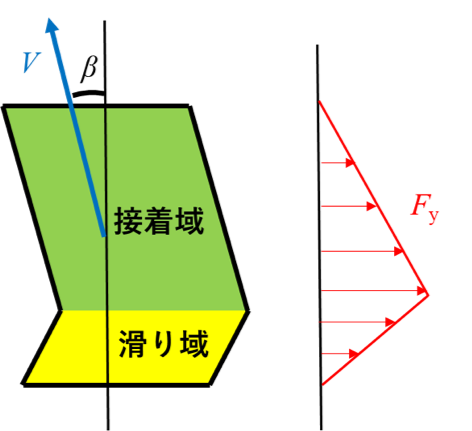
図6 横力発生時の接地面
さらに、タイヤ表面に一つ赤色の点をつけたときの接地面の時間変化を、図7に示す。
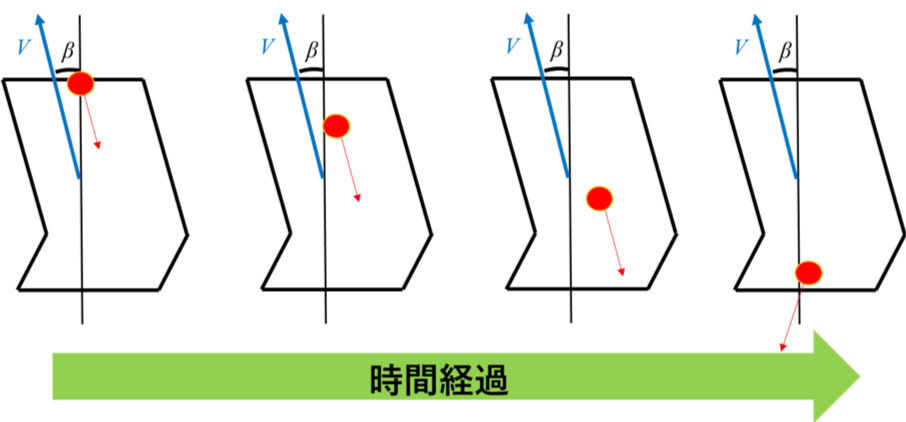
図7 接地面のタイヤ上の点の時間変化
スリップアングルが小さいときは接着域が支配的であり、スリップアングルが大きくなるにつれ滑り部の影響が無視できなくなる。滑り部は、接着域と比較して摩擦係数が小さくなる。よって、滑り域が大きくなるにつれ摩擦力の増加が小さくなっていく。これにより、非線形域が生じる。
さらにスリップアングルが大きくなり滑り部が支配的となると、摩擦力はスリップアングルに対して変化せず一定値をとる。これらの現象は、前後力についても同様である。
前後力と横力が同時に発生している状態を、コンバインドスリップと呼ぶ。コンバインドスリップ状況では、スリップ角とスリップ率両方の値がタイヤの前後横力に影響する。
ゴムの接触面における摩擦について記述する。
ゴムは粘弾性という特殊な材料特性を示し、ゴム-路面間の摩擦においては、クーロンの法則として有名な の式が成り立たない。もちろんクーロンの法則が成り立つと仮定して静止摩擦係数、動摩擦係数、それぞれを用いることは解析上効果的ではあるが、適用範囲は限られている。
粗さを持った物体とゴムの間の摩擦を精度よく解析する手法は現在確立していないが、基礎理論は確立しているとされている。
その一端を、ここで紹介する。ゴムの摩擦力は(3)式で表されるように、凝着摩擦とヒステリシス摩擦が足しあわされたものであるとされる。
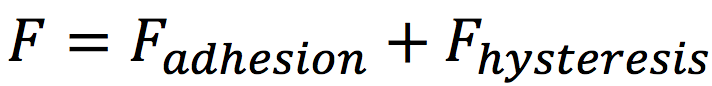
(3)式
F adhesion=凝着摩擦/F hysteresis=ヒステリシス摩擦
粗さを持った物体との接触面をミクロなスケールまで拡大すると、接触していない部分と接触している部分に分かれる。ここで、実際にゴムと路面が接触している面積を真実接触面積と呼ぶ。
真実接触面積は、ゴムと路面が分子的に接触している面積とも表現することができ、分子を横方向に引きはがすために力が必要となる。
この現象に依存する摩擦力を凝着摩擦といい、凝着摩擦は(4)式で表されるように、物体間の真実接触面積に比例するとされる。
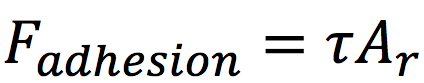
(4)式
t=せん断強さ/Ar=真実接触面積
一方、ヒステリシス摩擦は粘弾性特性によって生じる摩擦力である。粘弾性とはばねのように物体が変形した量のみに依存した力ではなく、ダンパーのように変形する速度にも依存して力を発生させるという特性である。
この特性によって、摩擦力が発生する。図7のようにゴム板の上に球を押しつけ、滑らせるという状況について考える。
速度を与えない図7(a)においては、ゴムから受ける反力の分布は前後対象となる。しかし図7(b)のように滑り速度を加えると、反力の分布は進行方向前方が大きく、後方が小さくなる。これによって進行方向と逆方向に、力が加わる。
これがヒステリシス摩擦である。
実際のタイヤにおいては、アスファルトの突起、目に見える大きさのものから肉眼では見えないものまで一つ一つが図のようになっている。
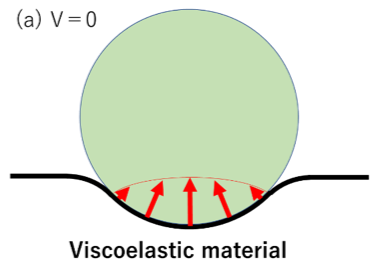
図7(a) ヒステリシス摩擦の概略
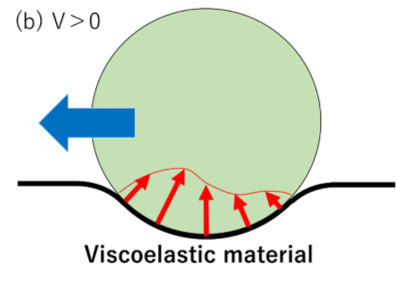
図7(b) ヒステリシス摩擦の概略
ヒステリシスの大きさを表すパラメータとして、tanδと呼ばれるものがある。
tanδは、周波数応答における力の虚部と実部の比としてあらわされるパラメータである。
変形におけるtanδは入力周波数や温度によっても変化する。
tanδが大きいほど損失されるエネルギーが大きくなるため、ヒステリシス摩擦が大きくなるが、一方で転がり抵抗が増え、燃費性能が下がるというデメリットがある。
これらの摩擦理論を原因として、一般的に使用されるタイヤにおいては、タイヤ接地圧が小さいほど局所的な摩擦係数が大きくなる。
車両全体の接地荷重の総和は(上下動や空力を除いて)常に一定であるため、接地面積を大きく、接地圧を均等にするほどに全体の摩擦係数が大きくなる。
そのため接地面積を増やすためにハイグリップタイヤであるほど溝が少なく、太くなる。
この摩擦係数の圧力依存性を活用することで、サスペンションやジオメトリ等を用いて全体のグリップ、ステアバランスの調整が可能である。
本章で説明した摩擦理論はあくまでオンロードでのものであり、オフロードではまた違う特性を示す。一例をあげると、スノーラリーで用いられるスパイクタイヤは、タイヤを細くすることでピンがよく食い込むようにしてグリップを確保する。
つまり接地圧を大きくした方が、摩擦係数を稼げるといった現状がある。
レース用タイヤは市販用タイヤと大きく異なる点がいくつかある。
まず一目でわかる点として、溝がないスリックタイヤである(一部を除く)ことが挙げられる。これは接地面積を大きくし、接地圧力を小さくすることでグリップ力を大きくするためである。
F1タイヤは一時期縦に溝が入ったタイヤ(通称グルーブドタイヤ)となったが、グリップを落として旋回速度を下げることが目的である。
F1のグルーブドタイヤの開発初期においてはグリップの減少のみではなく、摩耗の仕方が変化することによるライフの大幅な低下や、トレッド部の見かけの剛性が低くなることによる運動特性の劣化が問題となった。

レーシングタイヤ装着のフォミュラーカー
次に、tanδの値が大きく異なることが挙げられる。tanδのピークを高温時に大きくなるように設定して、レース中の高温のタイヤで大きいグリップ力を発生させる。
さらに、タイヤ表面が“溶ける”ようになっている。通常ゴムはエントロピー弾性と呼ばれる特性により、高温であるほど剛性が高くなる。しかし、レース用タイヤにおいてはコンパウンド部にオイルを混ぜることで熱を加えると柔らかくなるようになっている。そのため、走行後の熱を持ったタイヤは、べたべたしている。
走行時にタイヤが柔らかくなるようになり、真実接触面積が大きくなり、高いグリップを発揮する。
しかし、タイヤが温まらないとグリップが発生しないため、レースにおいてはウェービングなどによってタイヤを温める。走行時のトレッドの温度は、乗用車では40~80℃程度であるのに対して、レース用タイヤでは60℃~100℃程度といわれる。この温度に合わせてコンパウンドが設計されている。
レース用タイヤにおいては、グリップ力を得るために多くの工夫をしている一方で、騒音特性、長期の摩耗特性、乗り心地といった内容は無視したうえで設計されている。
ほかにも、力を発生させるときの過渡特性や、変形によって車両姿勢や空力に及ぼす影響の考慮もされている。
レース用タイヤの摩耗について簡単に記述する。
サーキットの路面、特に走行ライン上ではない部分にはタイヤカスがたまる。タイヤカスはグリップを終えたゴムが削れたものである。密度が低く、スカスカであるため、散らばっている見た目ほどにはタイヤは摩耗していない。
タイヤカスが飛ぶということはトレッド面に新しいゴムが出るということであり、グリップ力を持続させることにつながる。
また、走行後のタイヤ表面の摩耗跡から、タイヤがどのように使われたかが判断できる。
摩耗後のタイヤには、グレーニングと呼ばれるささくれ摩耗が生じる。
グレーニングは、グリップが足りない部分のタイヤに起こりやすい。オーバーステアが出ていればリアに生じやすく、アンダーステアならばフロントに生じる。
ささくれの方向も重要であり、滑りが生じていた方向の垂直方向にささくれが生じる。
周方向にグレーニングが生じていれば、そのタイヤが旋回時に滑っていたことがわかり、進行方向と垂直に発生していた場合はトラクション方向に滑っていたことがわかる。
ただし、減速時ブレーキを踏みすぎるとタイヤがロックしてしまう場合があり、その場合はタイヤの一部分のみが削れる。
ここで削れた部分をフラットスポットといい、タイヤがいびつな円形となって走行に悪影響を及ぼす。グレーニングは同一タイヤの中で部分ごとに方向やあれ具合が異なる場合もあり、タイヤの使われ方、つまり運転や路面との接地の仕方を見る指標にもなる。
タイヤはスリップアングルがついたらすぐに力を発生させるわけではなく、遅れが生じる。
タイヤが変形することによって、ホイールのスリップアングルの変化速度と接地面のスリップアングルの変化速度に差が生じるためである。
近似的に、線形域( が成り立つ)についてのモデル化を行うと、接地面のスリップアングルSAは(5)式で表せる。
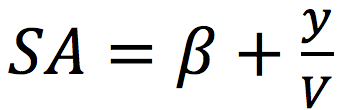
(5)式 β=スリップアングル/ y=変位速度/V=車両速度/ CP=コーナリングパワー
この式を用いてホイールのスリップアングルβから接地面のスリップアングルSAへの伝達関数を計算すると一時遅れ系となる。その時定数Tは(6)式で表せる。
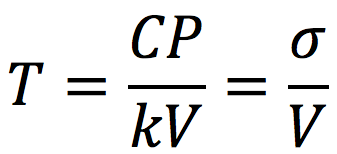
(6)式 CP=コーナリングパワー/K=タイヤ横剛性/V=車両速度
ここで、を、緩和長と呼ぶ。
は長さの次元を持つ。(6)式より、コーナリングパワーが大きいほど、タイヤの横方向剛性が小さいほど、速度が低いほど応答遅れが大きくなることがわかる。
現在、様々なメーカーで新しいタイヤの開発が進められている。
有名なところでは、
・空気が必要ない“エアレスタイヤ”
・パンクしても走り続けることが可能な“ランフラットタイヤ”
ほかにも、ダンロップでは路面状況に応じてトレッド部の特性が変化する“アクティブトレッドタイヤ”の開発がされている。
さらに、横浜ゴムが開発した車両空力を改善するフィンタイヤはすでにSuper GTで試されている。
これからEVや自動運転が発展していき、自動車の在り方が大きく変わっていくと考えられるが、タイヤは変わらず必要とされる。
車を支えるタイヤという部品が、さらに進化していくことに期待したい。
本コラムの内容を知っても、何かに役だつということはほとんどないかもしれません。
しかし本コラムで、タイヤの奥深さのほんの一端を知って下されば幸いです。
今回紹介はできませんでしたが、変形や振動、材料についてなどタイヤの要素はまだまだたくさん存在します。
本コラムについて、私は学生であり、専門家ではありませんので間違い等あるかもしれませんがその点はご容赦ください。
最後まで読んでいただいたことへの感謝をもちまして、本コラムを終了させていただきます。
(執筆:横浜国立大学フォーミュラプロジェクト(YNFP))